担当:塩士 圭介(日本海コンサルタント)

Q:アンケートの配布数を検討しているのですが、何通配れば良いのでしょうか?有効回答数はどの程度必要ですか?

A:必要な有効回答数は調査目的によって変わりますが、まずは統計的な考え方を理解し、必要となる有効回答数を基に、予想される回収率を逆算してアンケート配布数を設計しましょう。
はじめに
公共交通に関するアンケート調査を企画する際、「何通配布すれば良いのか?」「どの程度の回答数があれば信頼できる結果が得られるのか?」という疑問は、多くの実務者が抱く共通の悩みです。
以前の記事「住民に対するアンケート調査の実施はどのように実施したら良いですか」では、「誰に聞くか」「どのように聞くか」「何を聞くか」の重要性について触れましたが、今回は「何通の回収を取れば良いのか」という根本的な疑問に対して、統計的な考え方を踏まえながら、アンケート初心者の方にも分かりやすく解説します。
地域公共交通に限らず、様々な施策立案においてアンケート調査は重要な手法ですが、適切なサンプル数の設計なしには、せっかくの調査結果も根拠のない数字の羅列になってしまいます。統計的な裏付けを持った調査設計の考え方を身につけることで、より説得力のある調査結果を得ることができるでしょう。
なお、統計学の知識がどうしても必要となるため、一部に数式が登場してしまいますが、計算自体は表計算ソフトでも簡単に出来ます。
アンケート調査におけるサンプル数の基礎知識
母集団と標本の関係
アンケート調査では、調査対象全体を「母集団」、実際に調査する対象を「標本(サンプル)」と呼びます。例えば、A市の住民全体(5万人)が母集団だとすると、実際にアンケートに回答してくれた住民(例:500人)が標本となります。
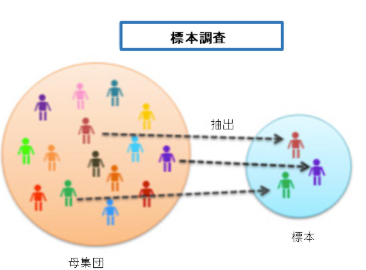
統計学では、この標本から得られた結果を用いて、母集団全体の傾向を推定します。しかし、標本は母集団の一部でしかないため、必ず「誤差」が生じます。この誤差をどの程度まで許容するか、どの程度の信頼性を求めるかによって、必要なサンプル数が決まります。
必要サンプル数の計算式
一般的に使用される必要サンプル数の計算式は以下の通りです。(いきなり数式が出てきますが、この数式は避けて通れないので、深く理解しなくてもいいので「こういうもんだ」という程度で押さえておけば良いです。)
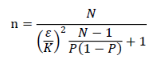
ここで、
- n:必要サンプル数(=回収が必要となる値)
- N:母集団(≒調査対象範囲の全人口・世帯、など)
- K:信頼度係数(95%信頼度の場合はK=1.96)
- ε:許容誤差(例:5%の場合は0.05)
- p:予想される回答の割合(不明な場合は0.5を使用すると最も安全なサンプル数を確保できます。)
許容誤差と信頼度の意味
許容誤差(ε)とは、調査結果にどの程度の「ブレ」を許容するかを示します。例えば、アンケートで「バスを利用したい」と回答した人が30%だった場合、許容誤差5%であれば、実際の母集団では25%~35%の間に真の値があると解釈します。
信頼度係数(K)は、この推定がどの程度確からしいかを示す係数です。上記で「95%信頼度の場合は」とありますが、これは同じ調査を100回実施した場合、95回は許容誤差の範囲内に真の値が収まることを意味します。K:信頼度係数の1.96は95%信頼度の時に使う係数で、正規分布という統計学の知識が必要なので説明は省略します。この信頼度の値及びを動かすことは実務上ほぼないため、K=1.96というものを代入するのだ、ということだけ覚えていてください。
ここまでで拒否反応を示す方も多いかも知れません。そこで、上記から計算される必要とされるサンプル数(有効回答数)のグラフを下につけておきます。
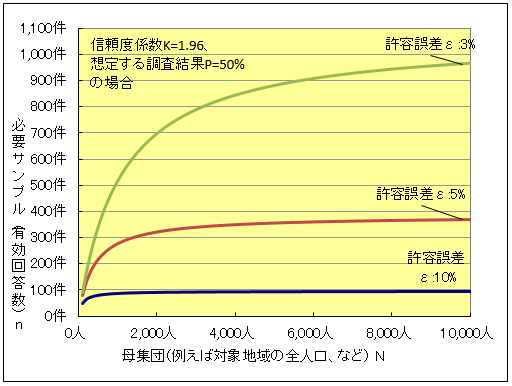
母集団を変化させたとき、必要となる有効回答数は、許容誤差(ε)によって大きく変わる一方で、母集団(対象地域の全人口)が大きくなっても、必要サンプル数は一定に収束することが分かります。一般的なアンケートでは、許容誤差ε=5%とする場合が多いため、このグラフから読み取れることは、対象人口の多さにかかわらず、350件程度の有効回収があれば良い、ということになります。
回収率を考慮した配布数の設計
回収率の現実的な見積もり
さて、有効回収数が分かったら、実際に「何通配布すれば良いのか?」ということを逆算せねばなりません。
アンケートの回収率は調査方法や対象者によって大きく異なりますが、おおよそ下記のとおりだと考えます。
- 郵送アンケート(一般住民):20~40%
- 郵送アンケート(利用者限定):30~50%
- インターネットアンケート(不特定多数に配布する場合):10~30%
- 対面・車内配布:50~80%
近年、郵送アンケートの回収率は低下傾向にあるため、25~30%程度を見込んでおくのが現実的です。また、自治体・地域によって大きく差が出る場合もあり、過去の当該自治体・地域におけるアンケート回収率も把握しておくことをオススメします。
配布数の逆算
必要な有効回答数から配布数を逆算する式は以下の通りです:
配布数 = 必要な有効回答数 ÷ 予想回収率
例えば、400件の有効回答が必要で、回収率を30%と見込む場合: 配布数 = 400 ÷ 0.3 = 1,334通 となり、安全を見込んで1,500通程度の配布を計画することになります。
調査目的別のサンプル数設計
全体傾向の把握が目的の場合
自治体全体の交通行動の傾向を把握したい場合は、前述のグラフのとおり、統計的な必要サンプル数(350~400件程度)を目安とします。この場合、比較的少ないサンプル数でも全体の傾向は把握できます。
地域別・属性別の比較が目的の場合
地域別や年齢層別の比較を行いたい場合は、各カテゴリーで最低100件程度のサンプルが必要と考えてください。(グラフでいうところの許容誤差ε=10%を想定。本来ならば、各地域・属性ごとに許容誤差ε=5%程度としたいところですが、そうすると配布数が増えすぎるため、地域・属性ごとの細かい集計には、ある程度の誤差を許容するという考え方です。)
例えば、5つの地域で比較を行いたい場合:
- 各地域100件 × 5地域 = 500件
- 回収率30%として:500 ÷ 0.3 = 1,667通の配布が必要
公共交通利用者の詳細把握が目的の場合
公共交通の利用率が低い地域では、無作為抽出による調査では利用者のサンプル数が不足します。
例:公共交通の利用率3%の地域で、利用者100件のサンプルが欲しい場合
- 必要な全体サンプル数:100 ÷ 0.03 = 3,333件
- 回収率30%として:3,333 ÷ 0.3 = 11,111通の配布が必要
と膨大な数を配布することとなり、無作為抽出のアンケート調査としては著しく非効率です。このような場合は、利用者に限定した調査(バス車内配布など)を併用することが効果的です。
予算制約下でのサンプル数調整
現実的な制約への対応
理論的に必要なサンプル数が算出できても、予算や時間の制約により、計画通りに実施できない場合があります。その際は以下の対応策を検討しましょう:
- 調査方法の工夫:郵送とWebの併用で回収率向上を図る。例えば、QRコードを印刷しておくことで、紙での提出が面倒と思う人(特に若年層)でも、スマホで簡単に回答出来る可能性が高まります。
- ターゲットの絞り込み:全住民ではなく特定層に限定
- 段階的調査:予備調査で傾向を把握してから本調査を実施
- 許容誤差の見直し:許容誤差を5%から例えば7%に変更することで必要サンプル数を削減。ただし、この場合は地域・属性別のクロス集計は統計的有意性が落ちることに注意してください。
サンプル数と調査精度のバランス
サンプル数が少なくても、調査設計や分析方法を工夫することで有効な結果を得ることは可能です。重要なのは、限られたサンプル数でできることとできないことを明確にし、結果の解釈に注意を払うことです。
調査計画設計上の注意点
代表性の確保
統計的に十分なサンプル数を確保しても、回答者が母集団を代表していなければ意味がありません。年齢構成や居住地域の偏りがないか確認してください。(必要に応じて重み付けによる補正を行う場合もなくはないですが、単純集計がしづらくなるため、あまりオススメしません。重み付け補正をしなくても良いように、地域バランス等を勘案した配布計画が必要です。)
無回答バイアスへの対応
アンケートに回答しない人と回答する人では、意識や行動に差がある可能性があります(無回答バイアス)。このバイアスを完全に排除することは困難ですが、以下の点を調査設計時に考慮することで、その影響を軽減できます:
- 回収率の向上策:再依頼状(兼御礼状)の送付、謝礼の検討、調査票の簡素化
:特に「調査票の簡素化」については、アレもコレも聞くと回収率の低下に繋がるので、調査のアウトプットをイメージしながら、出来ればA4×4ページ以内(=A3両面2つ折りに収まる範囲)が望ましいです。 - 調査方法の多様化:郵送・Webなど複数の回答手段を提供(前述)
- 結果解釈時の注意:回答者の属性分布を確認し、偏りがないかチェック
- 他の調査との比較:既存の統計データや他地域の調査結果との整合性を確認
無回答者の特性を直接把握することは困難ですが、これらの配慮により、より代表性の高い調査結果を得ることが可能になります。
調査実施時期の配慮
公共交通の利用状況は季節や曜日によって変動します。調査時期や天候条件による影響も考慮して調査日を選定しましょう。特に、学校が休みになる期間(8月)や、豪雪地帯で冬期に調査を行う場合など、季節バイアスがかかる可能性を考慮してください。ズバリ、オススメは10月頃、または5月連休明け~7月頃です。(気候が平均的と思われる時期に調査を実施することは一定の合理性はあると思います。)
参考:抽出率から考えるサンプル数設計(非推奨)
アンケート設計時に、「全人口からの抽出率を何パーセントにすればいいのか?」と聞かれることがたまにあります。
抽出率とは
抽出率は、母集団に対してどの程度の割合でサンプルを抽出するかを示します。
抽出率 = サンプル数 ÷ 母集団数 × 100
例えば、人口5万人の自治体で500人にアンケートを配布する場合、抽出率は1%となります。
抽出率の目安
実は、「抽出率」に決まった目安があるわけではありません。重要なのは抽出率の高さではなく、前述のとおり、統計的に必要な「有効回答数」を確保することです。
例えば、人口5万人の自治体で400件の有効回答が必要な場合、抽出率は約0.8%となりますが、人口5千人の自治体で同じ400件が必要な場合は抽出率は8%となります。母集団の規模に関わらず、統計的に必要なサンプル数は同程度であるため、母集団が小さいほど抽出率は高くなります。
ということで、アンケートを設計する上で、「抽出率」というのは統計的にはあまり意味をなさない、と言っても過言ではないと思われます。
おわりに
アンケート調査におけるサンプル数の設計は、統計的な理論と現実的な制約のバランスを取りながら進める必要があります。まずは調査の目的を明確にし、それに応じて必要なサンプル数を算出し、そこから回収率を考慮して配布数を決定するという一連の流れを理解することが重要です。
「とりあえず1,000通配布」ではなく、「この調査では○○を明らかにしたいので、△△件の有効回答が必要、そのためには□□通の配布が必要」という論理的な設計を心がけましょう。
また、サンプル数の多さが必ずしも調査の質の高さを意味するわけではありません。適切な調査設計と丁寧な分析があってこそ、限られたサンプルからも価値のある知見を得ることができます。
公共交通の計画策定において、住民の声を適切に把握し、それを施策に反映させるためには、根拠のある調査設計が不可欠です。今回紹介した考え方を参考に、より説得力のあるアンケート調査を実施していただければと思います。